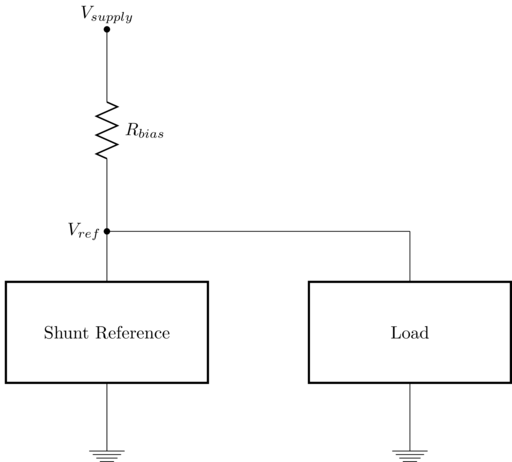
Discussion
The bias resistor for a shunt reference must guarantee that current through the reference never falls below its minimum operating current.
Shunt reference works by sinking precisely the right amount of current to establish voltage \(V_{ref}\) on its reference lead:
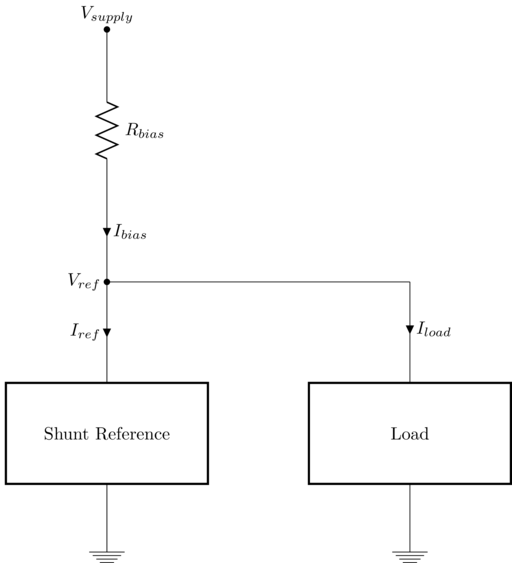
\(I_{ref}\) is required to remain above the minimum reference operating current \(I_{refmin}\); the maximum value for the minimum reference operating current, \(I_{refmin(max)}\), is given in datasheet. The lowest value of \(I_{ref}\) occurs when supply voltage is at a minimum, reference voltage is at a maximum and load current is at a maximum.
Component parameters that determine minimum viable value of the external resistor are:
- Maximum reference voltage \(V_{ref(max)}\)
- Maximum of minimum reference operating current \(I_{refmin(max)}\)
- Minimum supply voltage \(V_{supply(min)}\)
- Maximum load current \(I_{load(max)}\)
Therefore:
\[\begin{aligned} I_{ref} & \ge {{V_{supply(min)} - V_{ref(max)}} \over R_{bias}} - I_{load(max)} \ge I_{refmin(max)} \\ \Rightarrow R_{bias} & \le {{V_{supply(min)} - V_{ref(max)}} \over {I_{load(max)} + I_{refmin(max)}}} = R_{bias(max)} \end{aligned}\]
Both the bias resistor and the voltage reference will dissipate some power.
\[\begin{aligned} P_{bias} & = {V_{bias}^2 \over R_{bias}} \\ & = {(V_{supply} - V_{ref})^2 \over R_{bias}} \\ & \le {(V_{supply(max)} - V_{ref(max)})^2 \over R_{bias(min)}} = P_{bias(max)} \\ P_{ref} & = V_{ref} I_{ref} \\ & = V_{ref} ({{V_{supply} - V_{ref}} \over R_{bias}} - I_{load}) \\ & \le V_{ref(max)} {{V_{supply(max)} - V_{ref(max)}} \over R_{bias(min)}} = P_{ref(max)} \end{aligned}\]
Acknowledgements
This calculator and the discussion are based on Maxim Application Note 4003.